Math reveals how skateboarders can ramp up their half-pipe power
Skaters can quickly gain height — and energy — by crouching at key places along the ramp

Half-pipes look like a stretched-out letter U with a flat bottom. Skaters can do awe-inspiring tricks on them — but only if they’re going fast enough. Moving between crouching and standing — a pattern called pumping — is key to generating and maintaining that speed. Math shows how to optimize this.
Ben Welsh/The Image Bank/Getty Images
A new study hints at how skateboarders can up their half-pipe game — using math.
Tricks like kickflips and ollies require speed. As skateboarders roll along a U-shaped ramp called a half-pipe, they build speed and climb higher by pumping. To pump, they alternate between crouching and standing.
Pumping on a half-pipe is a lot like pumping on a swing, says Florian Kogelbauer. A mathematician, he works at ETH Zurich in Switzerland. On a swing, you stretch your legs while leaning backward and bend your knees while leaning forward. This motion changes how your body mass is distributed. Syncing your pumps with the back-and-forth motion of swinging gives you an energy boost that makes you go higher. This increases your potential energy. Pumping on a half-pipe does something similar for skateboarders.
Where should skateboarders change positions to get the biggest boost? Some say it’s about practice and feeling the rhythm. Kogelbauer and his colleagues instead turned to math.
They used a theoretical study. In this type, you first take a real-world problem and translate it into equations, Kogelbauer says. Then you solve these math problems and translate the answer back to the real world.
The researchers started with the equations for a simple case: a rider going back and forth on a swing. Most aspects of swinging are well understood: the forces at play, the motion and the energy involved. The scientists then modified these equations to better match the skateboard scenario. They used them to create a mathematical model. How far up the ramp a skater can go depends on how their body position changes along the half-pipe. This model captured that relationship.
Then they programmed their simple model into a computer. They added real-world details. These included things such as the size of the half-pipe and that of the skateboarder. Then this computer model calculated the ideal body position for skaters as they moved along the ramp’s length.
Skateboarders should crouch as they go downhill and stand just before they hit the flat area, this model suggests. Then they should crouch again until they hit the uphill. There, they should stand again and stay standing until they start to roll back downhill.
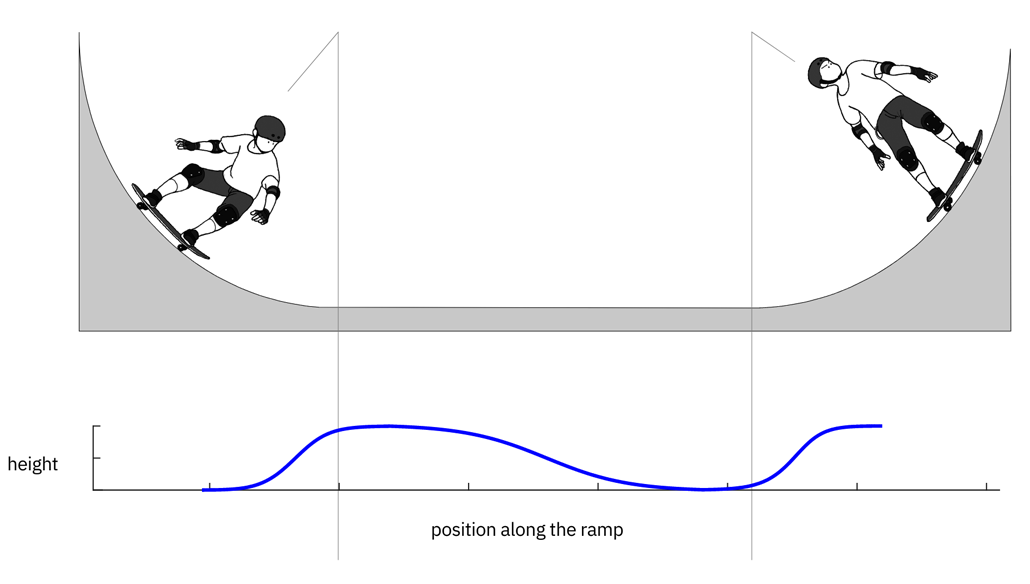
Simple models of real-world motion
The next step was to compare the model’s output against how real skateboarders move. The researchers recruited two skaters to tackle a half-pipe. The scientists instructed them to reach a certain ramp height as quickly as possible. Afterward, the team analyzed videos of the skaters’ motion to see where they crouched and stood.
The more experienced skater naturally pumped just like the team’s model suggested — and hit the goal height faster. The less experienced skateboarder had to pump more times to reach the same height. And that skater’s body position didn’t match the model very well.
That means the model likely captures the most efficient way to pump, Kogelbauer concludes. If you want to get better at skating half-pipes, he says, try to crouch and stand just as the model shows. The researchers shared their results in August in Physical Review Research.
This research could also benefit robotics, says Sorina Lupu. An engineer, she studies ways to help robots walk at the California Institute of Technology in Pasadena. People can contort their bodies in a huge variety of ways. Robots, however, lack muscles. This limits their range of motion, she explains. And that makes it harder to program complex movements in them, such as walking.
Some groups analyze human motion with high-tech equipment. Then they use artificial intelligence and machine learning to help robots copy that motion. It can pay off, but the model for the robots’ motion can get complicated. And if something goes wrong, it can be hard to figure out what happened and why, Lupu says.
But the skateboard study used a simple model to predict how someone should move. It worked even though it didn’t include all the complicated forces involved. That approach, she says, might work for robotics, too.
“There’s a lot of value in the work that they have done,” says Lupu. She especially likes that the team checked its model’s result against an experienced skateboarder’s motion.
The agreement shows that simple systems can model real-world motions well, says Kogelbauer. And it suggests that such models could help both athletes and robots improve their performance.







